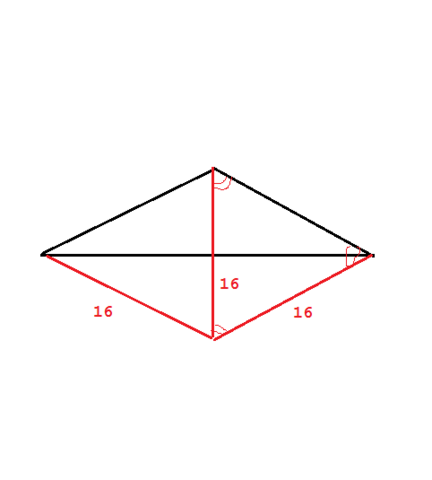
Если исходить из того, что ВСЕ боковые рёбра образуют угол в 45 градусов с высотой, получится, что их проекции на основание будут также равны 16 (т.к. треугольник "высота"-"ребро"-"проекция ребра" получится равнобедренным прямоугольным). Теперь нарисуем основание и нанесём всё то, что нам известно:
1. Точка-проекция верхней точки пирамиды будет лежать на линии из тупого угла, являющейся медианой/биссектрисой/высотой треугольника-основания.
2. Точка-проекция верхней точки пирамиды равноудалена от всех верщин основания на 16. Это значит, что она лежит ВНЕ треугольника основания - т.е. сама пирамида как бы нависающая.
Если это не очевидно (а центр окружности, описанной около тупоугольного треугольника, лежит вне его) - пишите, докажем отдельно.
Теперь рассмотрим треугольник, образованный боковой стороной основания, проекцией ребра из тупого угла и проекцией ребра из острого угла. Он равнобедренный, и один из углов при основании равен 120/2 = 60 градусов - ага, значит он не просто равнобедренный, но и равносторонний! Боковая сторона основания, таким образом, равна 16.
Дальше найдём "длинную" сторону основания - 2* 16*cos (30) = 32 *  /2 = 16
/2 = 16 
А опущенная на неё из тупого угла высота:
16*sin (30) =16 * 1/2 = 8
Площадь треугольника:
1/2 * a * h = 1/2 * 16  * 8 = 128
* 8 = 128 
Объём пирамиды:
1/3 * 128  * 16 = 2048/3 *
* 16 = 2048/3 *