1)найти область определения функций 2)определить четность,нечетность и периодичность...

Question

1)найти область определения функций 2)определить четность,нечетность и периодичность функций 3) найти координаты точек пересечения графика функций 4) найти промежутки знакопостоянства функций 5)найти промежутки возрастания и убывания,экстрэмумы 6)найти асимптоты кривой 7)построить график функций 8)используя построенный график функций,наити множество её значений f(x)=2x'2/(1+x'2) ; f(x)=x/(1-x'2)

Answer 1

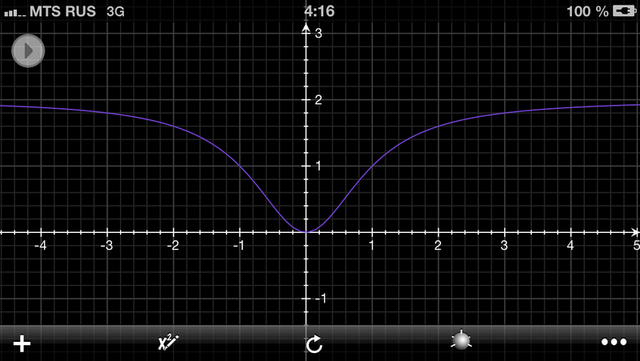
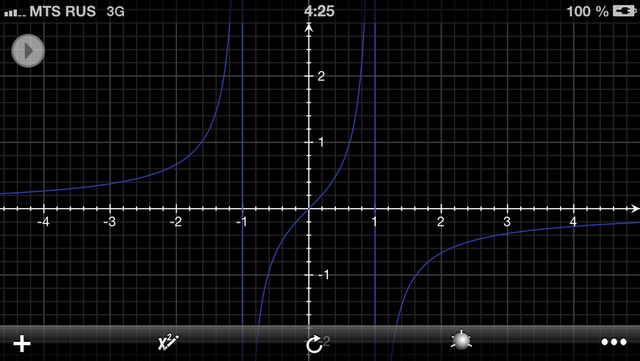
№1

f(x)=2x^2/(1+x^2)

1) D(y)=(-беск;+беск)
2) f(-x)= 2(-x)^2/(1+(-x)^2)=2x^2/(1+x^2)=f(x) => четная
    f(x+T)=2(x+T)^2/(1+(x+T)^2) не равно f(x) => непериодичная
3) C осью Ох:

y=2*0/(1+0)=0/1=0
(0;0)

C осью Оy:

2x^2/(1+x^2)=0
2x^2=0
x=0
(0;0)

4) y=0, если x=0
y>0, если x не равен 0
y<0 нет<br>
5) f'(x) = (4x(1+x^2) - 2x^2*2x)/(1+x^2)^2 = (4x+4x^3-4x^3)/(1+x^2)^2=4x/(1+x^2)^2=0
4x=0
x=0
    -           +
-----(0)----->x => x=0 - точка минимума

6) lim(2x^2/(1+x^2)) (x--->беск) = lim(2/(1/x^2 + 1)) (x--->беск) = 2/(0+1)=2
y=2 - горизонтальная асимптота
вертикальных асимптот нет.

7) Смотрите вложение №1

8) Е(y) = [0;2)


№2

f(x)=x/(1-x^2)

1) D(y) = (-беск;-1)U(-1;1)U(1;+беск)
2) f(-x) = -x/(1-(-x)^2)=-x/(1-x^2)=-f(x) => функция нечетная
непериодиная
3) С осью Ох:

y=0/(1-0)=0/1=0
(0;0)

C осью Oy:

x/(1-x^2)=0
x=0
(0;0)

4) y=0, если x=0
y>0, если x=(-беск;-1)U(0;1)
y<0, если x=(-1;0)U(1;+беск)<br>
5) f'(x)= (1-x^2 - x*(-2x))/(1-x^2)^2 = (1-x^2+2x^2)/(1-x^2)^2 = (1+x^2)/(1-x^2)^2 = 0
1-x^2=0
x^2=1
x=+-1
   +           +             +
----(-1)-------(1)------>  => функция возрастает на всей области определния

6) вертикальные асимптоты: x=-1; x=1

lim(x/(1-x^2)) (x--->беск) = lim((1/x)/(1/x^2-1)) (x---->беск) = 0/(0-1) = 0
y=0 - горизонтальная асимптота

7) Смотрите вложение №2

8) Е(y)=(-беск;+беск) 

---

---