В треугольник со сторонами 6, 10 и 12 вписана окружность. К окружности проведена...

Question

В треугольник со сторонами 6, 10 и 12 вписана окружность. К окружности проведена касательная, пересекающая две стороны треугольника. Какое наименьшее значение может быть у периметра треугольника, отсеченного этой касательной от исходного треугольника?

Answer 1

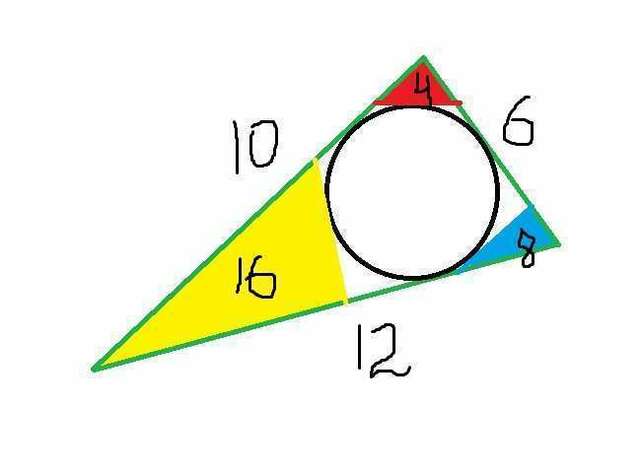
Периметр не зависит от положения касательной, а зависит от длины стороны данного треугольника, против которого расположена касательная. Периметр треугольника равен периметру данного треугольника минус удвоенная сторона.  Р(данного тр.) равен 28. Значит периметры отсеченного треугольника могут быть такими:
 28-6*2 =16,
28-10*2 = 8,
28-12*2 =4. 

---