ОПРЕДЕЛЕНИЕ
Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника плоскостью, а эту плоскость называют секущей плоскостью.
Отметим, что здесь мы рассмотрели взаимное расположение плоскости и выпуклого многогранника. Если многогранник невыпуклый, то плоскость может пересекать его по более сложным фигурам.
ПРИМЕР
Построить сечение пирамиды SABC плоскостью, проходящей через точки K, L и M, где K∈ABC, L∈ABC, а M∈ASC.
РЕШЕНИЕ (я покажу только начальное фото, как только открою доступ в лс - кину все фото)
Для решения этой задачи построим линии пересечения секущей плоскости с гранями пирамиды (эти линии называются следами секущей плоскости). Пусть плоскость сечения α уже построена. Так как плоскости ABC и α имеют две общие точки K и L, то они пересекаются по прямой KL.
Проведем прямую KL до пересечения с отрезками AB и BC в точках E и F. Пусть эта прямая пересекает прямую AC в точке X.
Далее рассуждаем аналогично. Плоскости ASC и α имеют две общие точки X и M, то есть они пересекаются по прямой XM. Проведем прямую XM до пересечения с отрезками SA и SC в точках H и G.
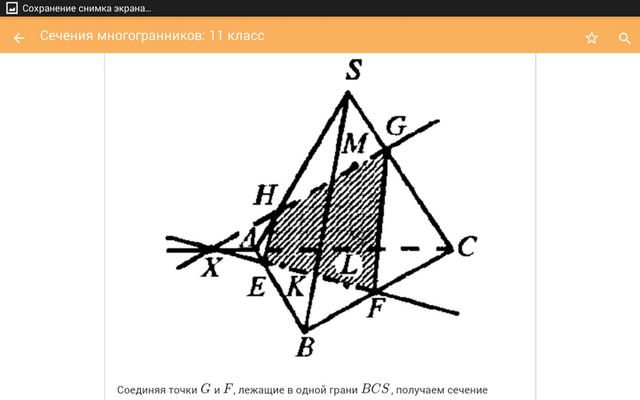
Соединяя точки G и F, лежащие в одной грани BCS, получаем сечение EFHG, единственность которого следует из аксиомы плоскости.