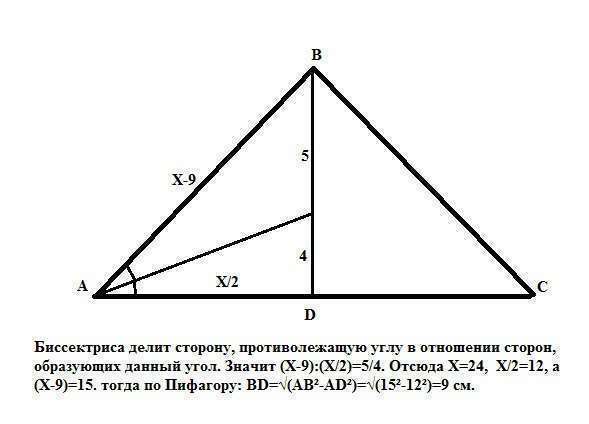
Пусть основание равно Х, тогда боковая сторона равна (Х-9).
В треугольнике, образованном высотой, проведенной к основанию, боковой стороной и половиной основания (данный нам треугольник равнобедренный) биссектриса угла при основании делит эту высоту в отношении 5:4, значит по свойству биссектрисы: "Биссектриса делит сторону, противолежащую углу в отношении сторон, образующих данный угол", имеем: (Х-9)/(Х/2)=5/4 или (9-Х)*2/Х=5/4. Тогда 8Х-72=5Х, отсюда Х=24. Итак, по Пифагору искомая высота равна
√[(Х-9)²-(X/2)²]=√(15²-12²)=9см.
Ответ: высота, проведенная к основанию, равна 9см.