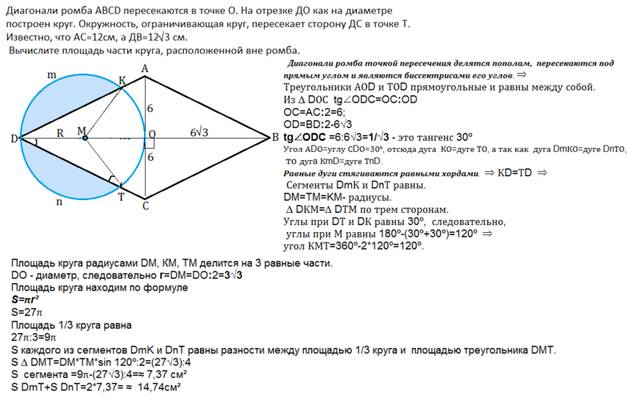
Пусть К - точка пересечения окружности с АD, М - центр окружности.
Диагонали ромба точкой пересечения делятся пополам, пересекаются под прямым углом и являются биссектрисами его углов. ⇒
Треугольники АОD и ТОD прямоугольные и равны между собой.
Из ∆ DОС tg∠ODC=OC:OD
OC=AC:2=6;
OD=BD:2-6√3
tg∠ODC =6:6√3=1/√3 - это тангенс 30º
Угол АDО=углу СDО, отсюда дуга КО=дуге ТО, а так
как дуга DmКО=дуге DnТО, то дугa КmD=дуге ТnD.
Равные дуги стягиваются равными хордами. ⇒
КD=ТD ⇒ Сегменты DmК и DnТ равны.
DM=TM=KM- радиусы.
Равнобедренные ∆ DКМ=∆ DТМ по трем сторонам.
Углы при DТ и DК равны 30º, следовательно,
углы при М равны 180º-(30º+30º)=120º ⇒
угол КМТ=360º-2*120º=120º.
Площадь круга радиусами DМ, КМ, ТМ делится на 3 равные части.
DО - диаметр, следовательно
r=DМ=DO:2=3√3
Площадь круга находим по формуле
S=πr²S=27π
Площадь 1/3 круга равна 27π:3=9π
S каждого из сегментов DmK и DnT равны разности между площадью 1/3 круга и площадью треугольника DМТ.
Ѕ ∆ DМТ=DМ*ТМ*sin 120º:2=(27√3):4
S сегмента =9π-(27√3):4=≈ 7,37 см²
S DmT+S DnT=2*7,37= ≈ 14,74см² - искомая площадь.