Решение:
1.
Найдём объём куба:
V=a^3 где а- ребро куба
V=10^3=1000 (см^3)
Объём шара равен:
V=4/3*πR^3 из этой формулы найдём радиус шара, подставив V=1000 (см^3)
1000=4/3*3,14*R^3
R^3=1000: (4/3*3,14)=1000*3:(4*3,14)=3000/12,56=238,85
R=∛238,85≈6,2 (см)
Ответ: Радиус шара равен 6,2см
2.
Объём шарового сектора равен:
Vсект.=2/3*πR^2*H
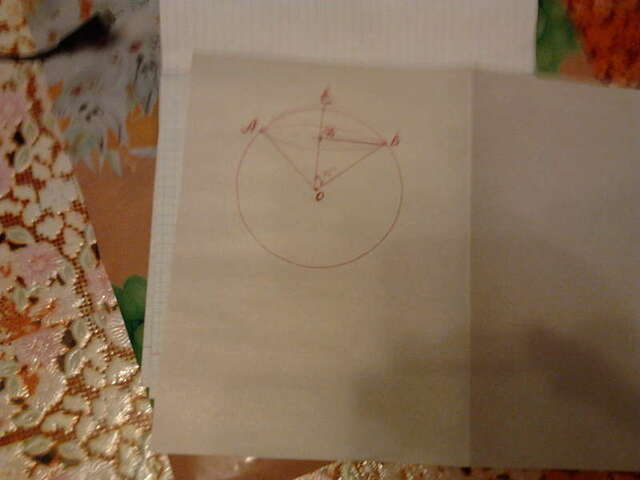
∠АОВ=90°
ОА=ОВ=ОС=R
Δ АОВ -равнобедренный прямоугольный треугольник
∠АОД=∠ВОД=45°
Из Δ ВОД следует:
cos∠ВОД=ОД/ОВ
Отсюда:
ОД=ОВ*cos∠ВОД=R*cos∠45°=√2/2*R
H=CД=СО-ДО=R-√2/2*R=(2R-√2*R)/2=R*(2-√2)/2
Отсюда:
Vсект.=2/3*πR² *R(2-√2)/2=πR³*(√2-2)/3
Ответ: Vсект.=πR³*(√2-2)/3
3.
V=V2-V1 где V-объём стенок; V1- объём внешнего, полного шара; V2- объём полого шара
Находим объём по формуле объёма шара:
V=4/3*πR³
V1=4/3*3,14*9³ = 18см:2=9см (радиус)
=4/3*3,14*729=4*3,14*243=3052,08 (см³)
V2=4/3*3,14*6³= 9см-3см=6см
=4/3*3,14*216=4*3,14*72=904,32 (см³)
Отсюда:
V=3052,08-904,32=2147,76≈2147,8(см³)
Ответ: Объём толщины стенок шара равен 2147,8см³