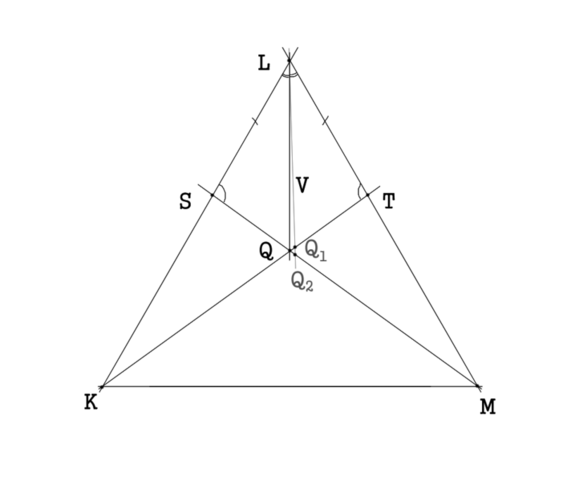
Проведём биссектриссу

для

Она пересечёт прямые

и

в точках

и

Мы пока не доказали, что все они совпадут с точкой

поэтому называемм их точками

и

Треугольники

и

равны по второму признаку равенства треугольников,
а значит

т.е. точки

и

совпадают, как мы и преполагали, образуя точку

в которой пересекаются

и биссектрисса

Отсюда следует, что

а так же

как вертикальные, а поэтому

и тогда

– по второму признаку равенства треугольников.
Т.е.

а

– равнобедренный.

По даказанныи равенствам треугольников:


Периметр

О т в е т :