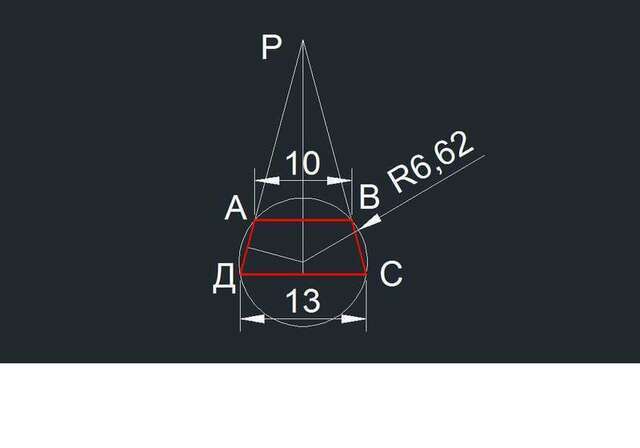
Решение удалось найти только для частного случая, когда четырёхугольник - это трапеция (а вписанная - только равнобедренная).
Примем основания трапеции равными заданным длинам сторон
АВ=10 СД=13.
Высота трапеции равна:
h = ((СД - АВ)/2)/tg15° = ((13 - 10)/2 )/(2-√3) = 1,5/0,267949 = 5.598076.
Боковая сторона равна а = √(((13-10)/2)²+h²) =
= √(1,5²+5.598076²) = √(2,25+31.33846) = √33.58846
= 5.795555.
Диагональ трапеции равна d = √((13/2)+(10/2))²+h²) =
= √(11,5²+5.598076²) = √
163.5885 = 12.79017.
Радиус окружности, описанной около трапеции, равен радиусу окружности, описанной около треугольника со сторонами, равными нижнему основанию трапеции, её боковой стороне и диагонали.
R = adc/(4√(p(p-a)(p-d)(p-c)).
Полупериметр р = (a+d+c)/2 = 15,694123.
Тогда радиус равен
R =
6.6092285.