Алиса хочет писать 6 чисел в кружке ** рисунке так чтобы Сумма чисел вершинах всех 5...

Question

Дан 1 ответ

gartenzie_zn · Answer 1 · 2018-04-18T18:06:24+0000

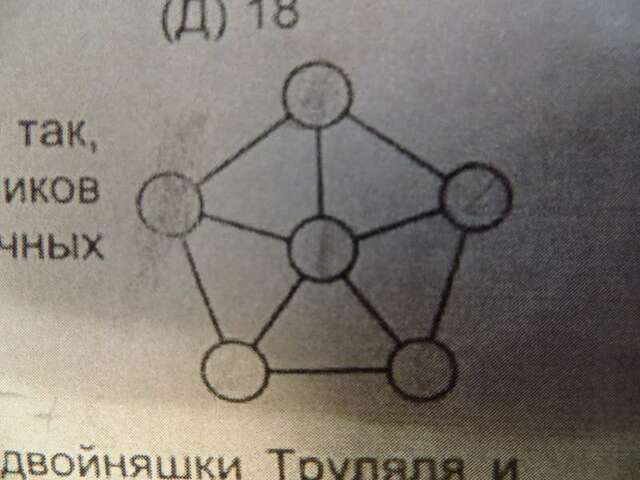
Обозначим все числа, начиная с того, что стоит в верхнем кружкке, по часовой стрелке, как   $a_1 \ , \ a_2 \ , \ a_3 \ , \ a_4 \$    и   $a_5 \ .$    Число, которое стоит в центре обозначим, как   $a_o \ .$

Равенство всех пяти сумм чисел, стоящих в вершинах треугольников, выражается уравнениями:

$a_o + a_1 + a_2 = a_o + a_2 + a_3 = a_o + a_3 + a_4 = a_o + a_4 + a_5 = a_o + a_5 + a_1 \ ;$

Заметим, что во всех суммах, помимо прочих (что можно легко понять и просто из рисунка) присутствует одно и то же число   $a_o \ .$

Так что это число может быть совершенно произвольным: простым, натуральным, целым, дробным, иррациональным, да хоть комплексным... Это ничего не изменит, поскольку данное число входит во все суммы в единичном экземпляре.

Вычеркнем из вышеозначенных уравнений проанализированное число и рассмотрим уравнения в упрощённом варианте:

$a_1 + a_2 = a_2 + a_3 = a_3 + a_4 = a_4 + a_5 = a_5 + a_1 \ ;$

Из первого равенста следует, что:

$a_1 + a_2 = a_2 + a_3 \ ; \Rightarrow a_1 = a_3 \ ;$

Из третьего равенста следует, что:

$a_3 + a_4 = a_4 + a_5 \ ; \Rightarrow a_5 = a_3 = a_1 \ ;$

Поскольку: $a_5 + a_1 = a_1 + a_2 \ ;$    то:   $a_2 = a_5 = a_3 = a_1 \ ;$

Из второго равенста следует, что:

$a_2 + a_3 = a_3 + a_4 \ ; \Rightarrow a_4 = a_2 = a_5 = a_3 = a_1 \ ;$

Таким образом, все «вершинные» числа должны быть равны между собой, а центральное при этом может быть каким угодно.

Значит на рисунке может оказаться одно или два различных числа.
Максимум : 2 .

О т в е т : 2 .