Дано:
KL=27
KN=24
MN=8
Найти: Р(KMN)=?
Решение
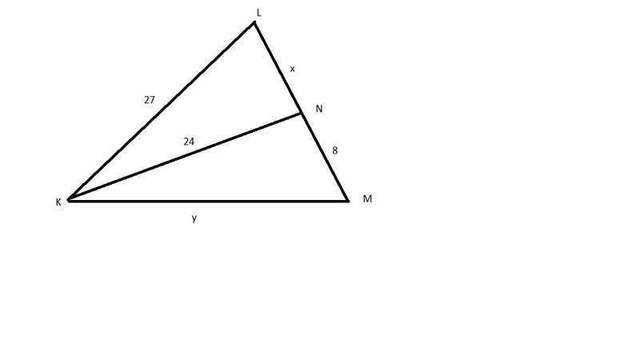
Пусть LN=x, а KM=y (рисунок
во вложении).
KN является биссектрисой в ΔKLM. Используя
свойство биссектрисы составим пропорцию: KL/LN=KM/MN.
По условиям задачи KL=27, MN=8, LN=x и KM=y. Подставим значения:
27/х=у/8
Выразим х*у:
х*у=27*8=216 (1)
Найдём длину биссектрисы KN:
KN²=KL*KM-LN*MN
По условиям задачи KL=27, MN=8, LN=x и KM=y
24²=27у-8х
576=27у-8х (2)
Решим систему уравнений:
{х*у=216
{576=27у-8х
Выразим значение х из первого
уравнения: х=216/у
Подставим его во второе уравнение
(метод подстановки):
576=27у-8х
576=27у-8*216/у
576=27у-1728/у (умножим все члены
на у, чтобы избавиться от знаменателя)
576*у=27у²-1728
27у²-1728-576у=0
27у²—576у-1728=0
D=b²-4ac=(-576)²-4*27*(-1728)=331776+186624=518400
(√D= 720)у₁=(-b+√D)/2a=(-(-576)+720)/2*27=1296/54=24
у₂=(-b-√D)/2a=(-(-576)-720)/2*27=-144/27 – не подходит,
т.к. х < 0
у=KM=24,
24х=216
х=LN=9
Р (ΔKMN)=KN+MN+KM=24+8+24=56
Ответ: периметр треугольника KMN равен 56.