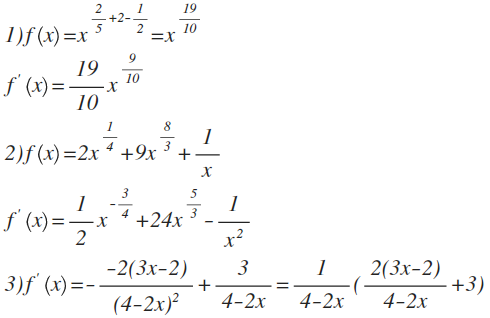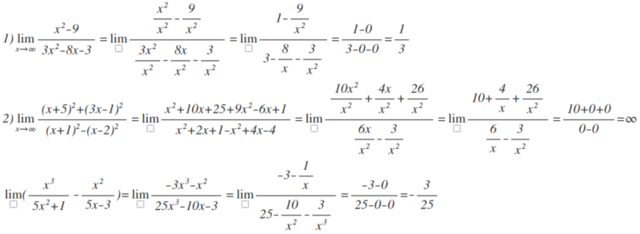1)y'=[(3x^5-5)^7]'(5x^3-3)+(3x^5-5)^7(5x^3-3)'=7(3x^5-5)^6*15x^4(5x^3-3)+(3x^5-5)^7*15x^2=
15x^2(3x^5-5)^6[x^2(5x^3-3)+(3x^5-5)^7]
2)f'(x)=(1/sqrt(x^2+1))'9x+(9x)'*1/sqrt(x^2+1)=-1/(x^2+1)*1/2*1/sqrt(x^2+1)*2x*9x+9/sqrt(x^2+1)=
9/sqrt(x^2+1)[1-x/sqrt[(x^2+1)^3]]
3)f'(t)=(t+1)'sqrt(t^2+1)+(t+1)(sqrt(t^2+1))'=sqrt(t^2+1)+(t+1)*1/2*1/sqrt(t^2+1)*2t=
sqrt(t^2+1)+t(t+1)/sqrt(t^2+1)
4)y'=1/2*1/sqrt(2x/(1+x))*(1/(1+x)^2*2x+2/(1+x))=1/sqrt(2x(1+x))(x/(1+x)+1
всего доброго