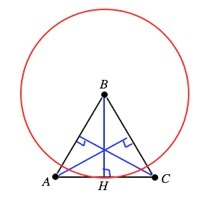
В равностороннем треугольнике все его биссектрисы равны и являются еще и медианами и высотами. Рассмотрим рисунок.
∆ АВС - равносторонний.
ВН - биссектриса и высота ⇒ ВН⊥АС.
ВН - радиус опружности с центром В по условию.
ВН перпендикулярен прямой АС, отрезок ВН - кратчайшее расстояние от центра В до прямой АС. ⇒
Н - единственная общая точка окружности и АС, следовательно, сторона АС ∆ АВС- касается данной окружности.
Аналогично доказывается нужное в отношении других сторон.