Сумма двух сторон треугольника,угол между которыми 60(градусов),равна 11 см,а длина...

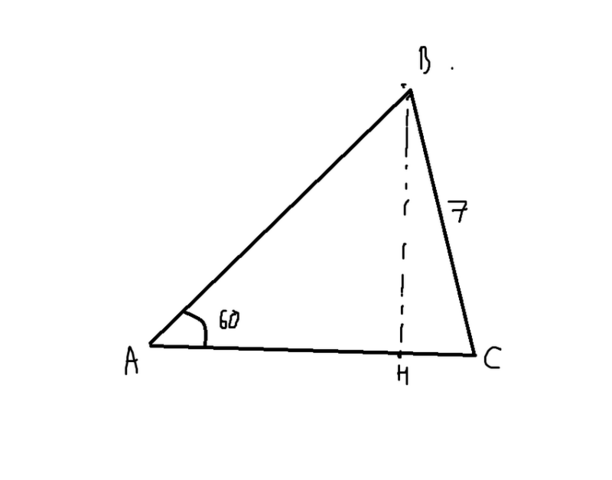
Имеем рисунок (во вложении)

$\sqrt{p(p-AB)(p-BC)(p-AC)} = \frac{AC\cdot AB \cdot sin60}{2}$

Так как AC = 11-AB и BC = 7, То уравнение принимает вид

$\sqrt{9(9-AB)(9-7)(9-11+AB))} = \frac{(11-AB)\cdot AB \cdot sin60}{2}$ (в левой части уравнения в третьей скобке не путаем знаки)

Полупериметр равен 9, так как 11+7 = 18.

Таким образом, аккуратно посчитав всё, что известно, и AB поместив в одну часть, находим AB и, затем вторую сторону.

Задача решена.