В основании правильной пирамиды лежит правильный многоугольник, а основание её высоты лежит в центре основания.
Все грани правильной пирамиды - равнобедренные треугольники.
Так как плоский угол при вершине равен 60º, то грани данной пирамиды - правильные треугольники, все её ребра равны.
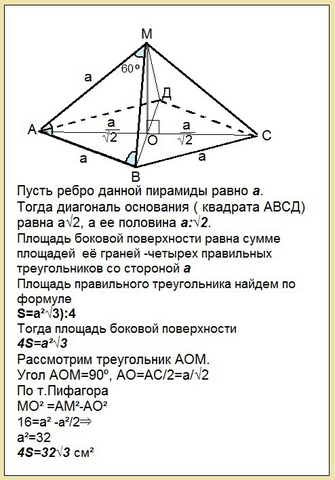
Пусть ребро данной пирамиды равно а.
Тогда диагональ основания ( квадрата АВСД) равна а√2, а ее половина а:√2.
Площадь боковой поверхности равна сумме площадей её граней -четырех правильных треугольников со стороной а
Площадь правильного треугольника найдем по формуле
S=a²√3):4
Тогда площадь боковой поверхности
4S=a²√3
Рассмотрим треугольник АОМ.
Угол АОМ=90º, АО=АС/2=а:√2
По т.Пифагора
MO² =АМ²-AO²
16=а² -а²/2⇒
а²=32
4S=32√3 см² - площадь боковой поверхности.