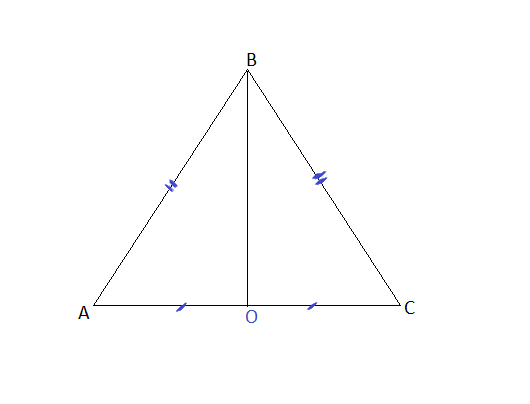Помогите решить задачи! 1.У равнобедреному трикутнику бічна сторона відноситься до...

Question

Помогите решить задачи!

1.У равнобедреному трикутнику бічна сторона відноситься до сторони як 5:6.Знайдіть площу трикутника якщо висота проведена до основи дорівнює 8см.?

2.Знайдіть кути ромба якщо його висотадорівнює 5 см.,а площа-50см.кв.?

Answer 1

1) Дан треугольник ABC

 

BO = 8

 

x*5/6 - боковая сторона

 

x - основание

 

Из треугольника ABO найдем по теореме Пифагора стороны: (x/2)^2 + 8^2 = (x5/6)^2

 

x^2 /4 + 64 -x^2*25/36 = 0

 

x^2 (1/4 -25/36) = -64

 

x^2 (9/36 -25/36) = -64

 

x^2(-16/36) = -64

 

x^2 = 36*4

 

x = 12

 

S = AC * BO /2= 12 * 8 /2= 96/2 = 48

 

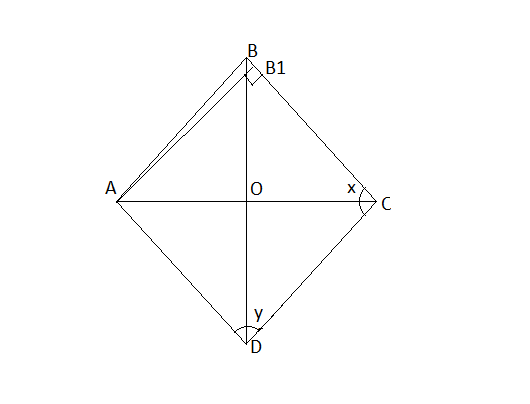
2) Дан ромб ABCD. AB1 - высота ромба, AB1 = 5, S_ABCD = 50

 

Найдем из площади сторону ромба: S_ABCD = AB1* AB

 

50 = 5 * AB

 

AB = 10

 

Теперь из другой формулы площади, найдём угол: S_ABCD = AB^2 * sin(y)

 

50 = 100 * sin(y)

 

1/2 = sin(y)

 

y = pi/6 + 2pi*n

 

y =  5pi/6 + 2pi*n

 

y = 30 или y = 150

 

Тогда x = 150 или 30

 

Углы ромба 30 и 150 градусов

 

 

---

---

Answer 2

1.Нехай бічна сторона 5х(а), а основа 6х(b)

S=48 2. Висота утворює прямокутний трикутник, де h - протилежний катет до кута A