Найдите наибольшее значение функции и значение аргумента, при котором функция это...

Question

Дан 1 ответ

Интереcующийся_zn · Answer 1 · 2018-04-22T14:35:57+0000

Без анализа здесь никак (хотя может и есть точнейшие методы решения таких задач). Прежде всего, думаем при каких значениях $x$ функция $y=f(x)$ не существует. То есть найдем такие значения $x$ , при которых выражение $f(x) = \frac{10-x}{3+\sqrt{x-1}}$ не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла:
1) знаменатель обращается в нуль:
Чтобы знаменатель обратился в нуль, нужно чтобы $3 + \sqrt{x-1} = 0$ , однако понятно, что $\sqrt{x-1} \geq 0$ , значит знаменатель не обратиться в нуль.
2) выражение под корнем в знаменателе будет отрицательным (корень из отрицательного числа не имеет смысла)
$x - 1 \ \textless \ 0 \\ x \ \textless \ 1$
Ага, имеем, что при любом значении $x\ \textless \ 1$ функции не существует. То есть она идет от $1$ и куда-то дальше. Куда — нам пока неизвестно.
Теперь посмотрим, что происходит с функцией при возрастании $x$ . Может быть она периодична?
$x = 1, y = 3 \\ x = 2, y = 2 \\ x = 5, y = 1$
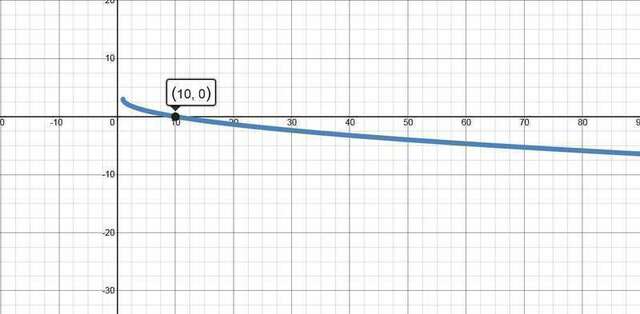
Пока что видим, что функция убывает. Найдем пересечение с нулем. Для этого просто найдем $x$ , при котором числитель обратиться в нуль. $x = 10, y = 0$
Попробуем вместо $x$ повставлять разные значения (большие и маленькие).
$x = 26, y = -2 \\ x = 50, y = -4 \\ x = 120, y = -8 \\ x = 850, y \approx -26 \\ x = 10000, y \approx -97$
Видим, что с увеличением $x$ уменьшается $y$ . Делаем вывод, что функция убывает бесконечно много. То есть $y_{max}$ — не существует, $x_{max}$ — не существует.

Найдите наибольшее значение функции и значение аргу­мента, при котором функция это...

Найдите наибольшее значение функции и значение аргумента, при котором функция это...