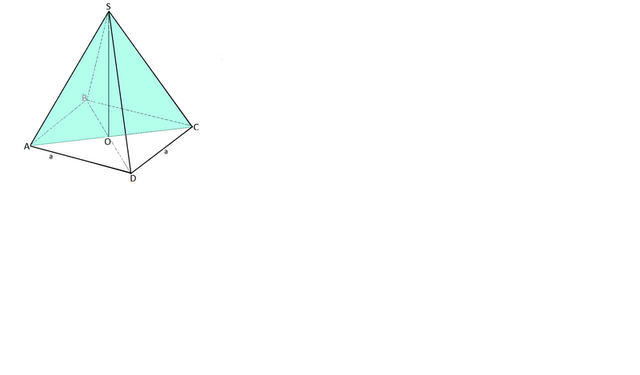
Cторона основания правильной четырехугольной пирамиды равна а, а ее диагональное сечение - равносторонний треугольник.
Найдите обьем пирамиды
Объём пирамиды равен одной трети произведения площади основания на ее высоту.
Площадь основания - площадь квадрата-
S ABCD=а²
Высоту найдем исходя из того, что диагональное сечение пирамиды - правильный треугольник АSС.
Стороной этого треугольника является диагональ АС основания.
Диагональ квадрата равна а√2
АС=АS=SC=а√2
Так как углы правильного трегуольника равны 60°, высота пирамиды
SO=АS·sin(60°)=(а√2·√3):2=а√6):2
Объем пирамиды
V={(а²·а√6):2}:3=(а³√6):6