50 баллов, надо решить в,г

Question

Дан 1 ответ

Правильный ответ

в)

Треугольник    $\Delta ABQ$     – равнобедренный, так как его боковые стороны образованы радиусами окружности. С другой стороны сумма углов любого треугольника равна    $180^o .$     А значит сумма оставшихся углов    $\angle QAB$     и    $\angle QBA$     равна    $120^o .$     В равнобедренном треугольнике углы при основании равны, а значит, эти углы равны между собой:

$\angle QAB = \angle QBA \ ;$

$\angle QAB + \angle QBA = 120^o \ ;$

Откуда следует, что:    $\angle QAB = \angle QBA = 60^o \ ;$

Стало быть, это не просто равнобедренный треугольник, а равносторонний. Т.е.:

$BC = AB = AQ = BQ = \sqrt{2} \ ;$

Углы    $\angle CAK \$     и    $\angle CKB \$     – опираются на одну и ту же дугу    $KB \ ,$     второй – как угол между хордой и касательной. Из этого следует, что:

$\angle CAK = \angle CKB \ ;$

В треугольниках    $\Delta CAK \$     и    $\Delta CKB \$     равны два угла (один у них общий), а значит эти треугльники подобны:    $\Delta CAK \sim \Delta CKB \ ;$

На этом основании составим пропорцию:

$\frac{AC}{CK} = \frac{CK}{BC} \ ;$

$AC \cdot BC = CK^2 \ ;$

$CK = \sqrt{ AC \cdot BC } \ ;$

Поскольку    $BC = AB \ ,$     то    $AC = 2AB = 2 \sqrt{2} \ .$

$CK = \sqrt{ AC \cdot BC } = \sqrt{ 2 AB \cdot AB } = \sqrt{ 2 AB^2 } = AB \sqrt{2} \ ;$

$CK = AB \sqrt{2} = \sqrt{2} \cdot \sqrt{2} = 2 \ .$

Кроме касательной    $CK \$     так же можно построить ещё и касательную    $CK' \$     по другую сторону от окружности. Заметим, что треугольники    $\Delta CKQ = \Delta CK'Q \ ,$     как прямоугольные по катету и гипотенузе, а значит, равны и    $CK = CK' \ .$

О т в е т : CK = CK' = 2 .

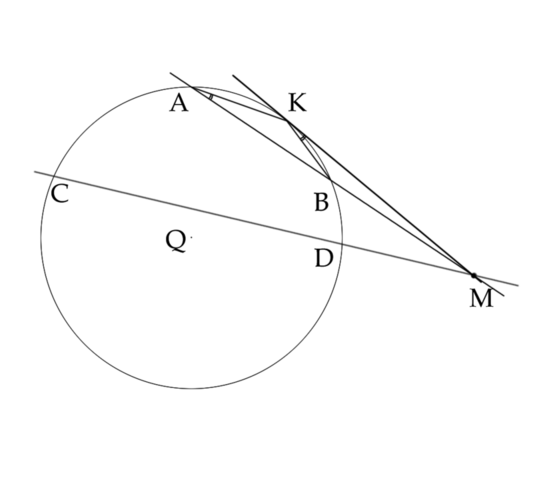
г)

Проведём касательную    $MK \$     из той же точки    $M \ .$

Углы    $\angle MAK \$     и    $\angle MKB \$     – опираются на одну и ту же дугу    $KB \ ,$     второй – как угол между хордой и касательной. Из этого следует, что:

$\angle MAK = \angle MKB \ ;$

В треугольниках    $\Delta MAK \$     и    $\Delta MKB \$     равны два угла (один у них общий), а значит эти треугольники подобны:    $\Delta MAK \sim \Delta MKB \ ;$

На этом основании составим пропорцию:

$\frac{MA}{MK} = \frac{MK}{MB} \ ;$

$MA \cdot MB = MK^2 \ ;$

Поскольку точки A и B были выбраны произвольно, то точно такие же рассуждения относятся и к точкам C и D с той же касательной MK. Из этого следует, что:

$MC \cdot MD = MK^2 \ ;$

Сопоставляя два последних равенства, получаем, что:    $MA \cdot MB = MK^2 = MC \cdot MD \ .$

$MA \cdot MB = MC \cdot MD \ ,$     что и требовалось доказать.

gartenzie_zn (8.4k баллов) 23 Апр, 18