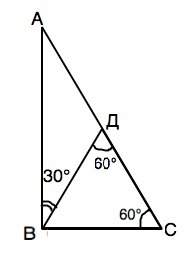
По условию угол С=60°.
Угол ВДС=60°. Из суммы углов треугольника третий угол ∆ ВДС=60°.
Треугольник ВДС - равносторонний.
Пр условию ∠АВД=30°, ∠ДВС=60° ( найдено) --
∠АВС=30°+60°=90°.
Тогда ∠ВАД=180°-∠АВС-∠АСВ=180°-90°-60°=30°
∆АДВ - равнобедренный ( по равным углам при основании АВ).
АД=ВД.
Но ВД=ВС=ДС⇒ АД=ДС=ВС. .
АС=АД+ДС=2 ВС.
АС противолежит бóльшему углу ∆ АВС ,⇒АС - наибольшая сторона этого треугольника. ⇒
АВ < АС.
Р(АВС)=АВ+АС+ВС=АВ+2ВС+ВС=АВ+3ВС
АВ<<strong>2ВС , следовательно, Р(АВС) < 5•ВС