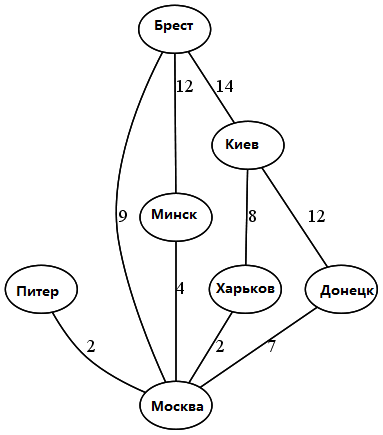
Для наглядности подписал условные города. (Без никаких намёков, серьёзно. Чисто ради наглядности).
Мысли есть такие: во-первых, карта содержит замкнутые маршруты - циклы, следовательно, может быть превращена в "дерево" методом отбрасывания части дорог. При этом общая протяжённость модернизируемых дорог будет сокращена, а сэкономленные денюжки можно будет распилить. Во-вторых, отбрасывание дорог (тем самым разрыв циклов) нужно сделать таким образом, чтобы исключалась самая длинная дорога. Вроде логика понятна.
Итак, попробуем. Идём слева направо.
Москва-Питер не имеет альтернатив, поэтому эту дорогу включаем в план модернизации. Далее видим цикл Москва-Минск-Брест-Москва. Какая из этих дорог самая длинная? Минск-Брест (12) - тогда исключаем эту дорогу из плана, но при этом связность городов сохраняется.
Следующий цикл остаётся Москва-Брест-Киев-Харьков-Москва. Отбросим Брест-Киев (14), как самую длинную. Далее остаётся последний цикл Москва-Харьков-Киев-Донецк-Москва. Здесь самая длинная дорога Киев-Донецк (12), исключаем её.
Больше циклов не остаётся, значит больше исключать никакую дорогу нельзя, иначе нарушится связность городов. Сколько исключили? 12+14+12.
Считаем оставшиеся: 2+9+4+2+8+7 = 32 -- такой ответ. Вроде так получается, проверь за мной внимательно.