Если сфера касается всех граней правильной треугольной призмы с ребром основания, равным...

0 голосов
608 просмотров

Если сфера касается всех граней правильной треугольной призмы с ребром основания, равным 2, то ее объем равен?

Геометрия (13.7k баллов) | 608 просмотров
Дан 1 ответ
0 голосов
Правильный ответ

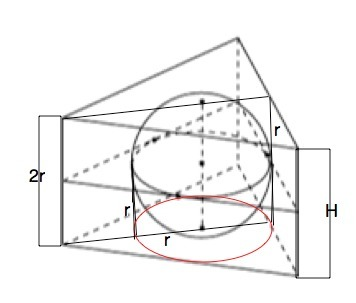
 Шар можно вписать в прямую призму в том и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.

 Если сфера касается всех граней правильной призмы, то высота призмы Н = 2r, r – радиус круга, вписанного в основание призмы.  Основание правильной треугольной призмы - равносторонний треугольник, все углы которого равны 60°. Радиус окружности. вписанной в него,  равен 1/3 его высоты h.

h=a*sin 60^{o} = \frac{2 \sqrt{3} }{2} = \sqrt{3}

r= \frac{ \sqrt{3} }{3} 

H=2r= \frac{2 \sqrt{3} }{3}

V=S•H

S= a^2 \frac{ \sqrt{3} }{4} } = \sqrt{3}

V= \frac{ \sqrt{3}*2* \sqrt{3} }{3}=2(ед. объема).

image
(228k баллов)
Похожие задачи