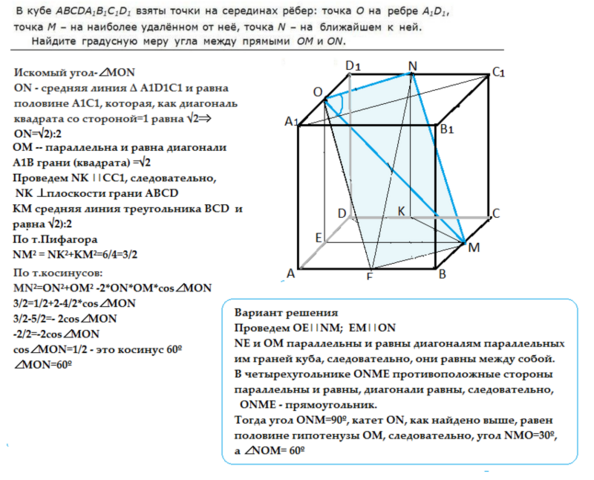
Примем ребро куба равным единице.
Соединив отрезками точки О, M, N, получим ∆ MON.
Искомый угол-∠MON
ОN - средняя линия ∆ А1D1C1 и равна половине А1С1, которая, как диагональ квадрата со стороной=1 равна √2⇒
ON=√2):2
ОМ -- параллельна и равна диагонали A1B грани (квадрата) =√2
Проведем NK ||СС1, следовательно, NK ⊥ плоскости грани АВСD
КМ средняя линия треугольника ВСD и равна √2):2
По т.Пифагора
NM² = NK²+KM²=6/4=3/2
По т.косинусов:
MN²=ON²+OM² -2*ON*OM*cos∠MON
3/2=1/2+2-4/2*cos∠MON
3/2-5/2=- 2cos∠MON
-2/2=-2cos∠MON
cos∠MON=1/2 - это косинус 60º
∠MON=60º
--------------
Вариант решения.
Проведем ОЕ||NM; EM||ON
NЕ и OM параллельны и равны диагоналям параллельных им граней куба, следовательно, они равны между собой.
В четырехугольнике ONME противоположные стороны параллельны и равны, диагонали равны, следовательно, ONME - прямоугольник.
Тогда катет ON треугольника ONM, как найдено выше, равен половине гипотенузы ОМ, следовательно, угол NMO=30º, а ∠NOM= 60º