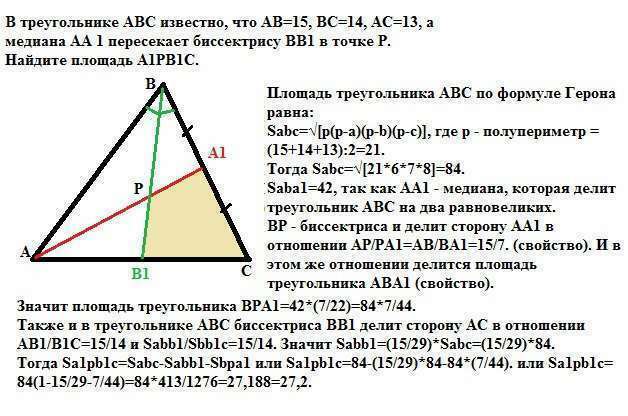
Площадь треугольника АВС по формуле Герона равна:
Sabc=√[p(p-a)(p-b)(p-c)], где р - полупериметр = (15+14+13):2=21.
Тогда Sabc=√[21*6*7*8]=84.
Площадь треугольника АВА1 равна: Saba1=42, так как АА1 - медиана, которая делит треугольник АВС на два равновеликих.
ВР - биссектриса и делит сторону АА1 в отношении
АР/РА1=АВ/ВА1=15/7 (свойство). И в этом же отношении делится площадь треугольника АВА1 (свойство).
Значит площадь треугольника ВРА1=42*(7/22)=84*7/44.
Также и в треугольнике АВС биссектриса ВВ1 делит сторону АС в отношении АВ1/В1С=15/14 и Sabb1/Sbb1c=15/14.
Значит Sabb1=(15/29)*Sabc=(15/29)*84.
Тогда Sa1pb1c=Sabc-Sabb1-Sbpa1 или
Sa1pb1c=84-(15/29)*84-84*(7/44) или
Sa1pb1c=84(1-15/29-7/44)=84*413/1276≈27,188≈27,2.