РЕШЕНИЕ
Для этого находим производную функции.
f(x) = 2x³ + 3x² - 12x + 4
f'(x) = 2*3*x(³-¹) + 3*2*x(²₋1) - 12*1*x(¹-1) = 6*x² + 6*x - 12
Производная положительная - функция возрастает
равна 0 = экстремум
отрицательная - функция убывает
Решаем квадратное уравнение и получаем корни
х1 = 1 и х2= -2
В переводе на результат = от -2 до -1 = производная отрицательна - функция
ОТВЕТ x ⊂[-2;0]
Дополнительно
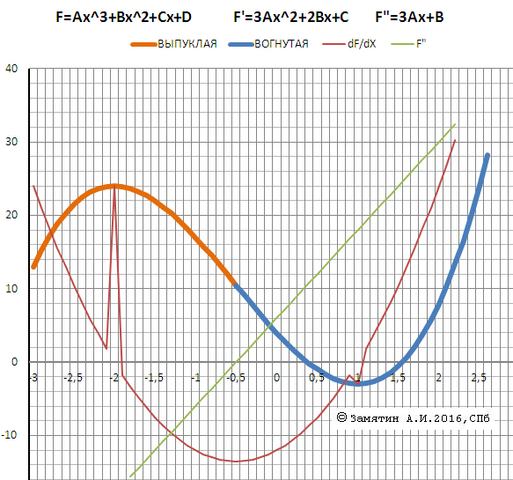
Fmax(-2) = 24 Fmin(1)= -3
И графики - функции и двух её производных