Длины отрезков,на которые диагональ трапеции делит среднюю линию,относятся как 3:7.Найти...

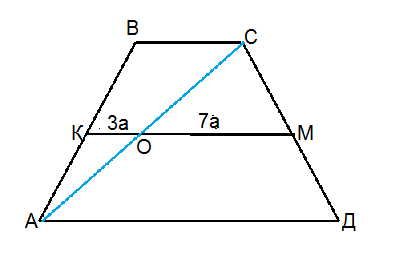
  Обозначим трапецию АВСД, среднюю линию -КМ, точку ее пересечения диагональю - О.
  Пусть коэффициент отношения отрезков средней линии будет а.
Тогда КО=3а, ОМ=7а.
КО- средняя линия ∆ АВС. ⇒ВС=6а
ОМ - средняя линия треугольника АСД⇒
АД=14а.
  По условию 14а-6а=20 см⇒
а=2,5 см
ВС=2,5*6=15 см
АД=2,5:14=35 см
35-15=20 см

Длины отрезков,** которые диагональ трапеции делит среднюю линию,относятся как 3:7.Найти...