Задание 1.
I способ.
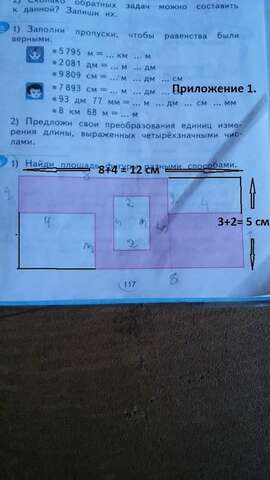
1) Дополни фигуру до прямоугольника (см. приложение 1):
Длина : 12 см = 8 см +4 см
Ширина : 5 см = 2 см +3 см
Площадь данного прямоугольника : S₀= 12×5 = 60 см²
2) Найдем площадь "белых" прямоугольников:
S₁= 4×3= 12 см²
S₂= 2×3= 6 см²
S₃= 2×4= 8 см²
Их общая площадь :
S₄= S₁+S₂+S₃= 12 см²+6 см²+8 см²= 26 см²
3) Найдем площадь фигуры:
S= S₀ -S₄= 60 см² - 26 см² = 34 см²
II способ.
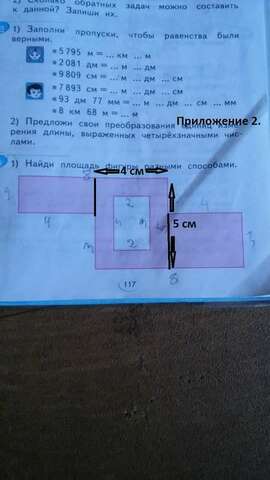
Разделим фигуру на прямоугольники ( см. приложение 2)
1) Площадь первого прямоугольника:
S₁= 2×4= 8 см²
2) Площадь второго прямоугольника:
S₂= 4×3= 12 см²
3) Площадь фигуры в центре:
Площадь прямоугольника : S₃= 4×5= 20 см²
Площадь "белого" прямоугольника: S₄= 2×3= 6 см²
Площадь фигуры в центре: S₅= 20 см² - 6 см²= 14 см²
4) Теперь найдем площадь фигуры на рисунке:
S= S₁+S₂+S₅= 8 см²+12 см² +14 см² = 34 см²
Задание 2. На мой взгляд , I способ - удобней.
Задание 3.
Если на рисунке 1 см = 2 м , тогда площадь 1 см² = 2 м ×2 м= 4 м². Мы уже нашли площадь фигуры на рисунке в см². ⇒
Площадь фигуры: S= 34 × 4 = 136 м ²
Проверим:
S= S₀ - S₄ =
= ( (12×2)× (5×2) ) - ((4×2) ×(3×2) + (2×2)×(3×2) + (2×2) × (4×2)) =
= 240 - ( 48 + 24 +32)= 240- 104= 136 м²
Задание 4.
Масштаб - это число, которое показывает во сколько раз реальные размеры предмета уменьшены ( или увеличены) на чертеже.
2 м = 2000 см⇒ т.е. 1 см на рисунке соответствует 2000 см в реальности.
Численный масштаб : 1 : 2000 .