Даю 50 баллов 1)** рисунке изображен график функции y=f(x) , определенной ** интервале...

Question

Даю 50 баллов
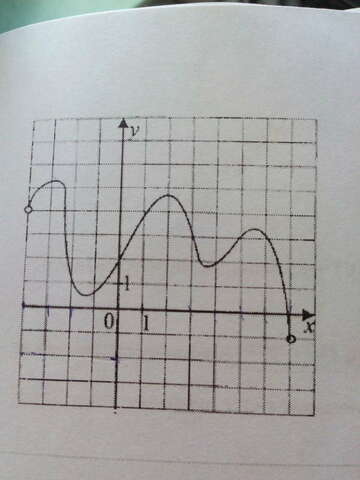
1)На рисунке изображен график функции y=f(x) , определенной на интервале (-4;7). Найдите количество точек, в которых касательная к графику функции
параллельна прямой y=-2
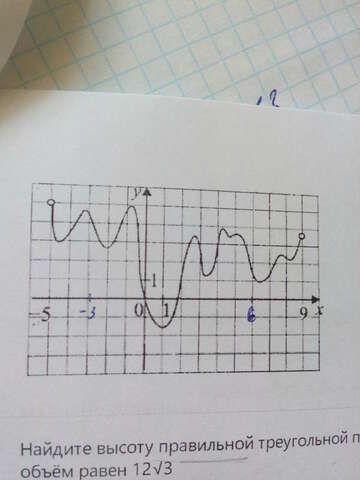
2)на рисунке изображен график первообразной y=F(x) некоторой функции y=f(x) , определенной на интервале (-5,9). Пользуясь рисунком , определите кол-во решений уравнения f(x)=0 на отрезке |-3;6| (квадратные скобки)

---

---

Answer 1

1. Общий вид прямой y = k*x + b, где k - коэффициент наклона этой прямой. У прямой y = - 2 этот коэффициент равен нулю. Коэффициент наклона касательной равен значению производной в точке касания, т.о. нам нужны точки, где производная будет равна нулю. Такие точки - точки экстремумом и перегибов. Перегибов тут нет, но есть 5 точек экстремумов. Т.о. ответ на первый вопрос - 5 точек.
2. Все рассуждения аналогичны п.1, нужные нам точки - перегибы и экстремумы. Таких точек на втором рисунке семь штук. Т.о. ответ на второй вопрос - 7

Answer 2

5 точек возможно я так думаю второе 

Comments

незнаю