Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле
r=(a+b-c):2
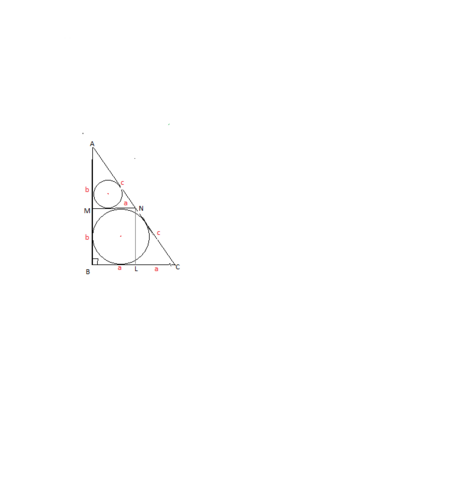
Проведем вторую среднюю линию NL, параллельную АВ и равную половине АВ.
Пусть стороны ⊿ АMN равны a,b,c,
тогда стороны⊿ АВС=2a, 2b, 2c, так как MN и NL - его средние линии.
Радиус вписанной в ⊿АМN окружности равен
r=(a+b-c):2
Cтороны ⊿АВС в два раза больше сторон ⊿ АMN, и радиус его будет:
R=(2a+2b-2c):2=2(a+b-c):2=(a+b-c).
R=2r, что и требовалось доказать.