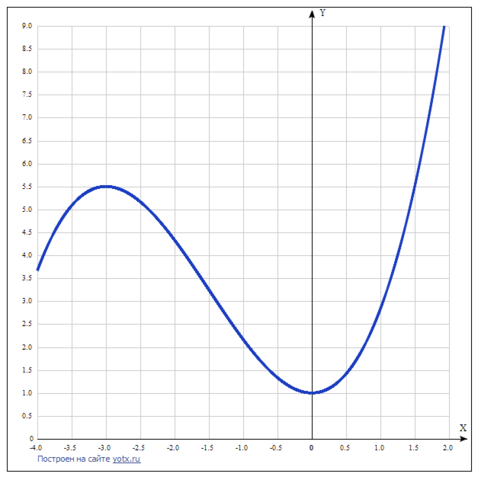
Находим производную функции y=(1/3)*x³+(3/2)*x²+1:
y ' = (1/3)*3x² + (3/2)*2x = x² + 3x = x(x+3).
Приравняв нулю производную, получаем 2 критические точки:
х = 0,
х = -3 эту точку не рассматриваем - она за пределами заданного отрезка.
Определяем свойства точки х = 0.
Находим значения производной левее и правее 0.
х = -1
0
1
y ' = -2 0 4.
Производная меняет знак с минуса на плюс - это минимум функции. Он равен у = 1.
Максимум находим на границах отрезка х=(-1; 1).
х = -1 0 1
y = 1.5 1 3.5.
Ответ: минимум функции равен у = 1 при х = 0.
максимум функции равен у = 3,5 при х = 1.