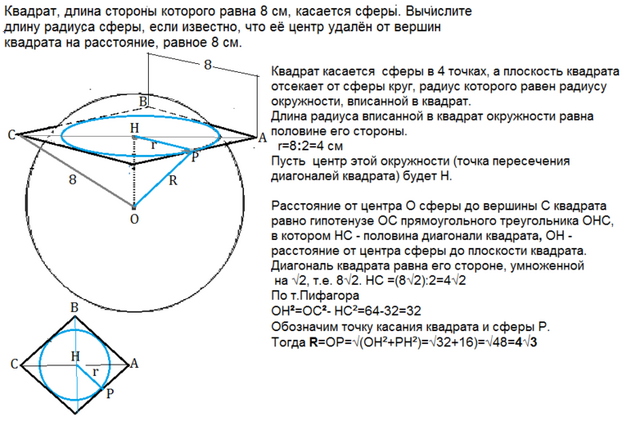
Квадрат, длина стороны которого равна 8 см, касается сферы. Вычислите длину радиуса сферы, если известно, что её центр удалён от вершин квадрата на расстояние, равное 8 см.
Квадрат касается сферы в 4 точках, а плоскость квадрата отсекает от сферы круг, радиус которого равен радиусу окружности, вписанной в квадрат. Длина радиуса вписанной в квадрат окружности равна половине его стороны.
r=8:2=4 см
Пусть центр этой окружности (точка пересечения диагоналей квадрата) будет Н.
Расстояние от центра О сферы до вершины С квадрата равно гипотенузе прямоугольного треугольника ОНС, в котором НС - половина диагонали квадрата, ОН - расстояние от центра сферы до плоскости квадрата. (см. рисунок)
Диагональ квадрата равна его стороне, умноженной на √2, т.е. 8√2. НС =(8√2):2=4√2
По т.Пифагора
ОH²=OC²-HC²64-32=32
Обозначим точку касания квадрата и сферы Р.
Тогда R=ОР=√(OH²+PH²)=√32+16)=√48=4√3 см