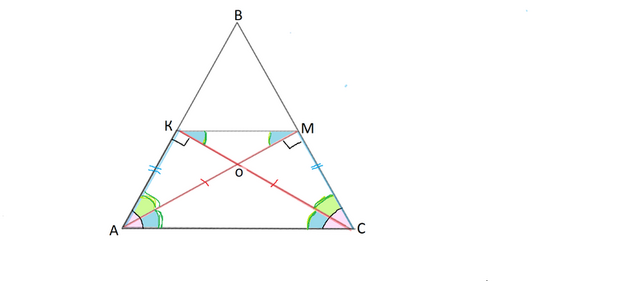
Рассмотрим треугольники АКС и СМА
Оба они - прямоугольные, имеют общую гипотенузу АС и равные острые углы:
∠А=∠С , т.к. треугольник АВС - равнобедренный и углы при основании АС равны.
Прямоугольные треугольники. в которых равны гипотенуза и острый угол - равны.
Из равенства этих треугольников следует, что
равны и треугольники АКМ и СКМ.
В этих треугольниках равны три стороны.
АМ=КС, АК=СМ, а КМ - общая.
Следовательно, углы КСМ=МАК
Но так как ∠А=∠С, то ∠ А - ∠МАК= ∠С- ∠КСМ.
Мы доказали равенсто углов КСА= МАС
Треугольники АОС и КОМ равнобедренные и подобны,
так как имеют равные стороны КО=ОМ, ОС=ОА, ∠ КОМ=∠АОС как вертикальные, и отсюда углы при основаниях этих треугольников равны ( 180 - ∠АОС):2.
Из подобия равнобедренных треугольников следует, что углы МКС=КСА и КМА=МАС.
Но эти углы - накрестлежащие при КМ и АС и секущих КС и МА.
Следовательно, КМ||АС, что и требовалось доказать.