Порой нужно доказать и очевидное.
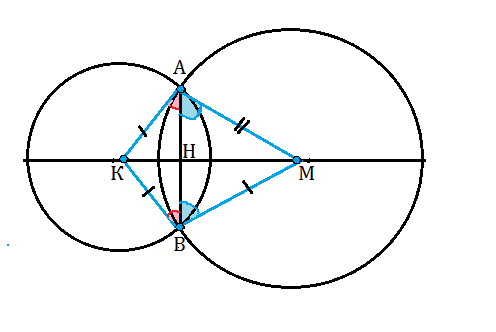
Обозначим центры окружностей К и М, а точку пересечения АВ и прямой КМ - Н.
Боковые стороны ∆ АКВ - радиусы, ⇒ ∆ АКВ - равнобедренный.⇒
∠КАВ=∠ КВА
Боковые стороны ∆ АМВ радиусы, ⇒ ∆ АМВ равнобедренный. ⇒
∠МАВ=∠МВА
В треугольниках КАМ и КВМ углы при А и В - сумма равных углов. ⇒
∠КАМ=∠КВМ
стороны КА=КВ, АМ=ВМ⇒
∆ КАМ=∆КВМ по двум сторонам и углу между ними. ⇒
∠АКН=∠ВКН, и ∆ АКН=∆ ВКН. ⇒
АН=ВН, и тогда КН - медиана равнобедренного ∆ АКВ, и его биссектриса и высота. ⇒
КН⊥АВ, что и требовалось доказать.