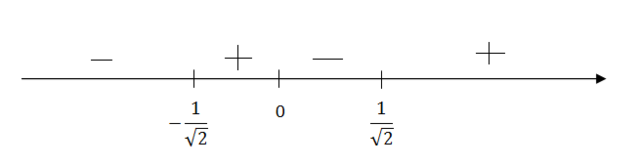Найти экстремумы:y=2x^4-2x^2

Question

Дан 1 ответ

2Stupid_zn · Answer 1 · 2018-04-24T17:25:05+0000

Краткий ответ:
$y=2x^4-2x^2$
$y'=(2x^4-2x^2)'=8x^3-4x$

t{2} " alt="8x^3-4x=0 \\ x(8x^2-4)=0 \\ x_{1}=0; \\ 8x^2-4=0 \\ 8x^2=4 \\ x^2=1/2 \\ x_{2}=1/ \sqrt{2} \\ x_{3}=-1/ \sqrt{2} " align="absmiddle" class="latex-formula">
$1) y(0)=2* 0^{4} -2*0^{2}=0 \\ 2) y( \frac{1}{ \sqrt{2} } )=2* \frac{1}{4} -2* \frac{1}{2} =- \frac{1}{2} \\ 3) y( -\frac{1}{ \sqrt{2} } )=2* \frac{1}{4} -2* \frac{1}{2} =- \frac{1}{2}$
Ответ: $0; - \frac{1}{2}$ .
Развернутый ответ:
$y=2x^4-2x^2$
Экстремумы функции - значение функции в точках экстремума (в точках минимума и максимума).
Найдем производную данной функции:
$y'=(2x^4-2x^2)'=8x^3-4x$
Найдем критические точки (критические точки - точки, в которых производна функции равна нулю или не существует). Для этого приравняем значение производной к 0:
$8x^3-4x=0 \\ x(8x^2-4)=0 \\ x_{1}=0; \\ 8x^2-4=0 \\ 8x^2=4 \\ x^2=1/2 \\ x_{2}=1/ \sqrt{2} \\ x_{3}=-1/ \sqrt{2}$
Отметим данные значения на числовой прямой (см. рис).
Найдем значение производной на каждом из промежутков, чтобы определить поведение функции (убывает или возрастает). Если производная y'>0, то функция возрастает; если производная y'<0, то функция убывает.<br>Для примера рассмотрим промежуток от $1/ \sqrt{2}$ до +∞.
Возьмем любое число из этого промежутка. К примеру, 1.
$y'(1)=8*1^{3} -4*1=8-4=4\ \textgreater \ 0$ , значит, функция возрастает на данном промежутке.
Аналогичным способом определяем поведения функции на других промежутках.
Поскольку при переходе через точку $x=\frac{1}{ \sqrt{2} }$ производная изменяет знак с "-" на "+", то эта точка является точкой минимума; при переходе через точку $x=0$ производная изменяет знак с "+" на "-", поэтому эта точка является точкой максимума; при переходе через точку $x=- \frac{1}{ \sqrt{2} }$ производная изменяет знак с "-" на "+", поэтому эта точка является точкой минимума.
Имеем 3 точки экстремума: $0, \frac{1}{ \sqrt{2} } , -\frac{1}{ \sqrt{2} }$
Найдем значение функции в точках экстремума, то есть найдем экстремумы функции:
$1) y(0)=2* 0^{4} -2*0^{2}=0 \\ 2) y( \frac{1}{ \sqrt{2} } )=2* \frac{1}{4} -2* \frac{1}{2} =- \frac{1}{2} \\ 3) y( -\frac{1}{ \sqrt{2} } )=2* \frac{1}{4} -2* \frac{1}{2} =- \frac{1}{2}$
Ответ: $0; - \frac{1}{2}$ .