Решите графическим способом систему уравнений: 1. (x+2y=-7 2. (x+y=2 (-2x+3y=7...

$\left\{\begin{matrix} x &+ &2y &= &-7 \\ x &+ &y &= &2 \end{matrix}\right.\\\\\\ \left\{\begin{matrix} 2y &= &-7 &- &x \\ y &= &2 &- &x \end{matrix}\right.\\\\\\ \left\{\begin{matrix} y &= & \frac{-7-x}{2} \\ \\ y &= &2-x \end{matrix}\right.$

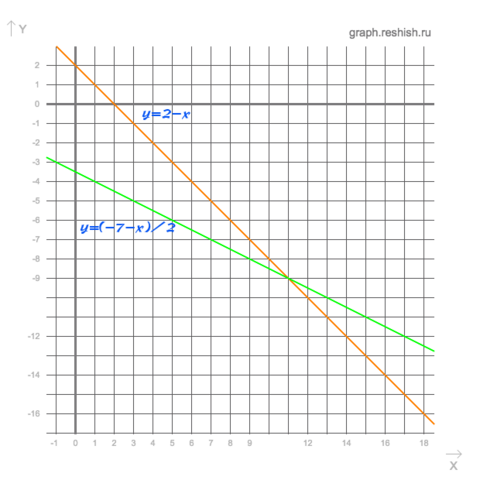
Строим график этих двух уравнений. Точка пересечения двух графиков будет являться решением системы.

Приложение во вложении.

Ответ: $(7;-9)$

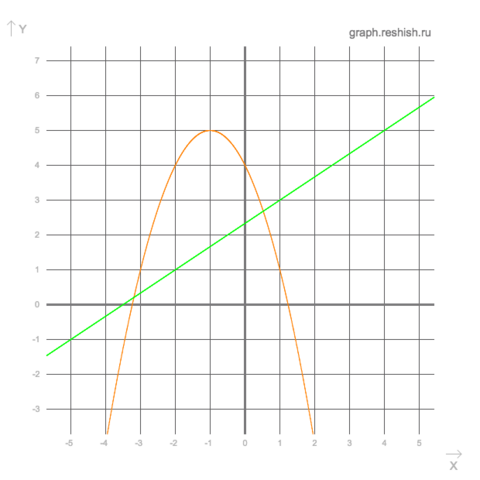
2) $\left\{\begin{matrix} -2x &+ &3y &= &7 \\ y&=&-x^2 &- &2x &+4 \end{matrix}\right.\\\\\\ \left\{\begin{matrix} 3y &= &7 &+ &2x \\ y&=&-x^2 &- &2x &+4 \end{matrix}\right.\\\\\\ \left\{\begin{matrix} y &=& \frac{7+2x}{3} \\ \\ y&=&-x^2 - 2x +4 \end{matrix}\right.\\\\$

Решим квадратное уравнение, чтобы найти точки пересечения с осями ОХ и вершину параболы:

$-x^2-2x+4=0\\ D=4+16=20; \sqrt D=2\sqrt5\\\\ x_{1/2}= \frac{2\pm2\sqrt5}{-2}= \frac{2(1\pm\sqrt5)} {-2} =-1\pm\sqrt5\\\\ x_1=-1-\sqrt5\\ x_2=\sqrt5-1\\\\$

Найдем вершину параболы:

$x_0= \frac{2}{-2}=-1\\\\ y_0= -(-1)^2-2\cdot(-1)+4=5$

Выполним построение обоих графиков (в приложении)

Во второй системе явно какая-то ошибка. Ответ неудачный