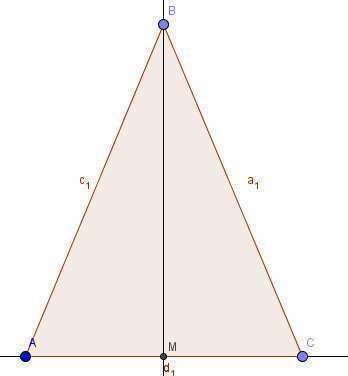
Проведем к основанию  равнобедренного треугольника
равнобедренного треугольника  медиану
медиану  (так как она медиана, то проходит из вершины
(так как она медиана, то проходит из вершины  в серидину
в серидину  и делит
и делит  пополам). Существует свойство, что медиана равнобедренного треугольника (а
пополам). Существует свойство, что медиана равнобедренного треугольника (а  по условию равнобедренный), проведенная к основанию также является и высотой. Отсюда
по условию равнобедренный), проведенная к основанию также является и высотой. Отсюда  .
.
Рассмотрим теперь  , он прямоугольный, как мы только что выяснили, один из его катетов нам известен —
, он прямоугольный, как мы только что выяснили, один из его катетов нам известен —  .
.
Найдем второй катет по теореме Пифагора:

Отлично. Теперь найдем  , это очень пригодится нам в дальнейшем. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. В нашем случае противолежащий углу
, это очень пригодится нам в дальнейшем. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. В нашем случае противолежащий углу  катет —
катет —  , а гипотенуза —
, а гипотенуза —  . Тогда
. Тогда  найдем как:
найдем как:
 .
.
Отлично! Все построения, описанные до этого момента вы можете увидеть на первом рисунке (он приложен к ответу, его можно найти в самом низу).
==========
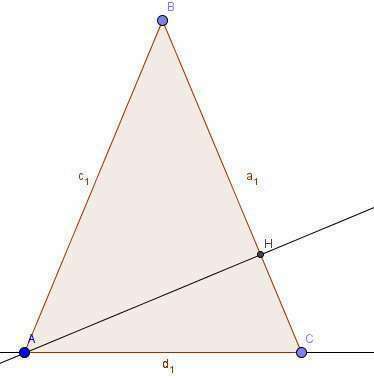
Теперь построим ту ситуацию, которая описана в задаче. Увидеть эти построения вы можете на втором рисунке.
Рассмотрим  . Он прямоугольный, так как
. Он прямоугольный, так как  — высота по условию. Известна гипотенуза
— высота по условию. Известна гипотенуза  , необходимо найти катет
, необходимо найти катет  .
.
Вот здесь нам и понадобится  . Напомню, что
. Напомню, что  — равнобедренный, а значит углы при основании равны (
— равнобедренный, а значит углы при основании равны ( ), а значит и их синусы тоже равны! То есть
), а значит и их синусы тоже равны! То есть  . Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. В
. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. В  противолежащий углу
противолежащий углу  катет —
катет —  , а гипотенуза
, а гипотенуза  . Отсюда:
. Отсюда:

Также нам известно, что 
Отсюда:

Отсюда выразим искомый катет  :
:


Это ответ.