№1
Рассмотрим треугольники ABE и BEC:
AB = BC, AD = DC (по условию)
BE - общая. следовательно
треугольник ABE = BEC. следовательно
стороны AE и EC равны.
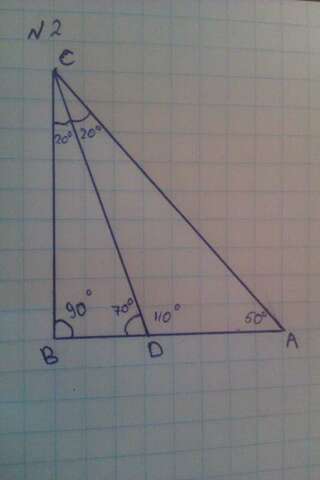
№2 рисунок во вложениях.
Дано: треугольник ABD
угол B = 90 градусов
CD - биссектриса
угол BDC = 70 градусов
Найти: Угол А и угол С
Сравнить: AD и CD
а) Рассмотрим треугольник BCD:
угол В = 90 градусов (по условию)
угод BDC = 70 градусов (по условию) следовательно
угол BCD = 180 - (90 + 70) = 20 градусов.
Рассмотрим треугольник ACD:
угол CDA = 180 - угол CDB (по св-ву смежных углов)
угол CDA = 180 - 70 = 110 градусов
угол DCA = угол BCD = 20 градусов (т.к. CD биссектриса)
угол A = 180 - (угол CDA + угол DCA)
угол А = 180 - (110 + 20) = 50 градусов
б) В треугольнике ADC против угла A лежит сторона CD
Против угла DCA лежит сторона AD
угол А = 70 уградусов
угод DCA = 20 градусов
Т.к. в треугольнике против большего угла лежит большая сторона, следовательно AD > CD
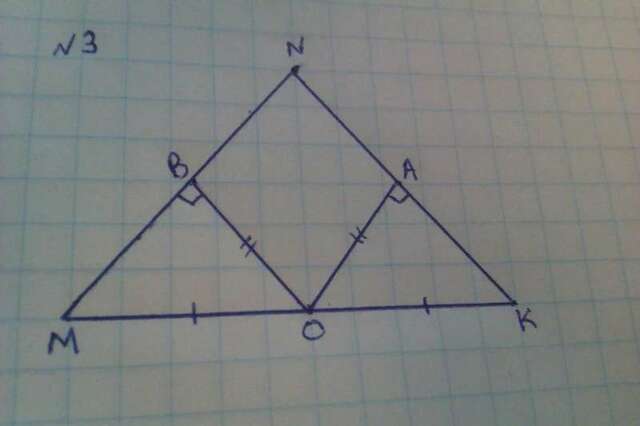
№3 рисунок во вложениях.
Дано: треугольник MNK
MO = OK
OA перпендикулярно NK, а OB перпендикулярно NM
OA = OB
Доказать, что треугольник MNK - равнобедренный
Рассмотрим треугольник MBO и OAK - прямоугольные, и равные по гипотенузе и катету. следовательно угол M равен углу К которые являются углами при основании треугольника MNK
Значит треугольник MNK - равнобедренный.