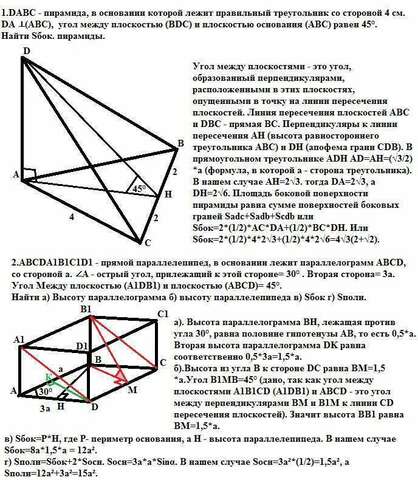
1).Угол между плоскостями - это угол, образованный перпендикулярами, расположенными в этих плоскостях, опущенными в точку на линии пересечения плоскостей. Линия пересечения плоскостей АВС и DВС - прямая ВС.
Перпендикуляры к линии пересечения АН (высота равностороннего
треугольника АВС) и DН (апофема грани СDВ). В прямоугольном треугольнике ADH AD=АН=(√3/2)*а (формула, в которой а - сторона треугольника).
В нашем случае АН=2√3. тогда DA=2√3, а
DH=2√6. Площадь боковой поверхности пирамиды равна сумме поверхностей боковых граней Sadc+Sadb+Scdb или
Sбок=2*(1/2)*АС*DA+(1/2)*BC*DH. Или
Sбок=2*(1/2)*4*2√3+(1/2)*4*2√6=4√3(2+√2).
2). а). Высота параллелограмма ВН, лежащая против угла 30°, равна половине гипотенузы АВ, то есть 0,5*а. Вторая высота параллелограмма DK равна соответственно 0,5*3а=1,5*а.
б).Высота из угла В к стороне DC равна ВМ=1,5*а.Угол В1МВ=45° (дано, так как угол между плоскостями А1В1СD (A1DB1) и АВСD - это угол между перпендикулярами ВМ и В1М к линии СD пересечения плоскостей). Значит высота ВВ1 равна ВМ=1,5*а.
в) Sбок=Р*Н, где Р- периметр основания, а Н - высота параллелепипеда. В нашем случае Sбок=8а*1,5*а = 12а².
г) Sполн=Sбок+2*Sосн. Sосн=3а*а*Sinα.
В нашем случае Sосн=3а²*(1/2)=1,5а², а Sполн=12а²+3а²=15а².