Фигура называется симметричной относительно прямой, если каждая точка этой фигуры имеет точку, симметричную ей риносительно данной прямой, которая принадлежит этой фигуре.
В таком случае прямая называется осью симметрии.
Если перегнуть фигуру по оси симметрии, иее части совпадут между собой, то данная фигура симметрична относительно данной оси симметрии.
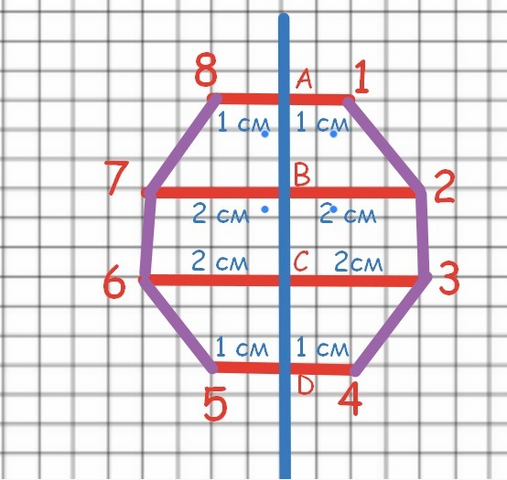
См. Чертеж во вложении:
Чтобы построить восьмиугольник, симметричный относительно прямой, нужно отметить произвольную точку 1 и опустить из нее перпендикуляр к прямой, обозначить получившийся отрезок |1A|, затем продолжить отрезок до точки 8, так что отрезок |A8|=|1A|.
Продожаем строить подобным образом отрезки: |2B|=|B7|; |3C|=|6C|;
|4D|=|D5|.
Соединяем точки 1→2→3→4→5→6→7→8 и получаем восьмиугольник, симметричный относительно данной прямой. Данная прямая делит восьмиугольник на 2 равных четырехугольника.
Проверка: можно вырезать данный восьмиугольник и перегнуть его по оси симметрии и, будет видно, что две части восьмиугольника (2 четырехугольника) совпадают.
Чертеж.