Имеем:  .
.
Найти наименьшее целое число, удовлетворяющие этому неравенству.
--------
1) Решим предложенное неравенство. Для этого:
1. Найдем корни. То есть решим уравнение  .
.



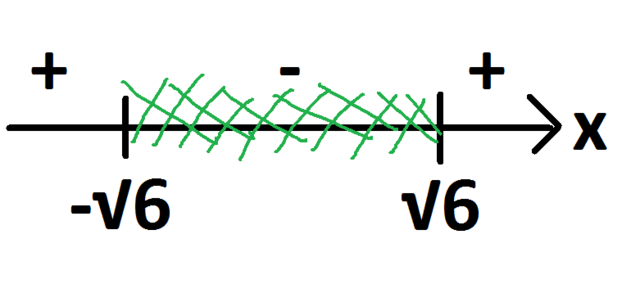
2. Нанесем корни на числовую ось и отметим интервалы (чередуем плюс и минус справа налево), выберем интервал‐решение (нас интересует интервал с минусом, так как неравенство меньше нуля):
смотрите приложенную картинку.
3. Запишем наше решение в виде интервала:

Неравенство решено. Теперь выполним вторую часть задания.
2) Найдем наименьшее целое число, удовлетворяющие неравенству. Разберемся, что от нас требуется.
1. Целые числа — это такие числа, у которых нет дробной части и которые могут быть как положительными (6, 10, 365), так и отрицательными (-1, -8, -10).
2. Наименьшее значит самое маленькое. Среди чисел 10, 5, 0, -5, число -5 будет наименьшим, посколько оно отрицательное.
3.  , то есть
, то есть  не целое число. Нужно найти такое целое число, которое будет самым близким к числу
не целое число. Нужно найти такое целое число, которое будет самым близким к числу  .
.
Итак, нам нужно найти такое целое число, которое будет отрицательным и находится ближе всего к числу  .
.
Так как  , то наименьшее целое число, которое входит в интервал решений нашего неравенства есть число
, то наименьшее целое число, которое входит в интервал решений нашего неравенства есть число  .
.
Итак, ответ: -2.