В параллелограмме противоположные углы равны, а сумма соседних равна 180° как сумма односторонних углов при пересечении параллельных прямых секущей.
∠А=∠С.
∠AВC+ ∠BСD=180°.
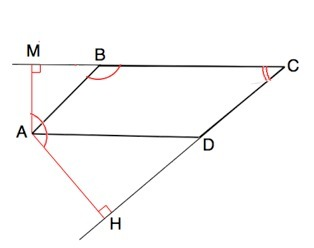
Проведя высоты АМ и АН к продолжению СВ и СD, получим четырехугольник СМАН, в котором углы АМС и АНС - прямые. Их сумма 90°•2=180°.
Сумма углов выпуклого четырехугольника 360°.
Сумма ∠МАН+∠ВСD=360°-180°=180° ⇒
∠AВC+∠BСD=МАН+ВСD, ⇒ ∠МАН=∠АВС, что и требовалось доказать.