Выясните при каких значениях X дробь х^4+7х^2+12/2х-х^2 положительна и при каких...

1)Для начала укажем область определения данной дроби:
2x-x²≠0
x(2-x)≠0
x≠0 и x≠2,так что:
x∈(-∞;0)v(0;2)v(2;+∞)

2) Разложим числитель на множители:
x⁴+7x²+12=0
Замена: x²=a
a²+7a+12=0
D=49-48=1
a₁=(-7+1)/2=-3;a₂=(-7-1)/2=-4
Обратная замена:
x²=-3 x²=-4
Решений нет,следовательно,числитель не раскладывается на множители,а все его значения всегда больше нуля.

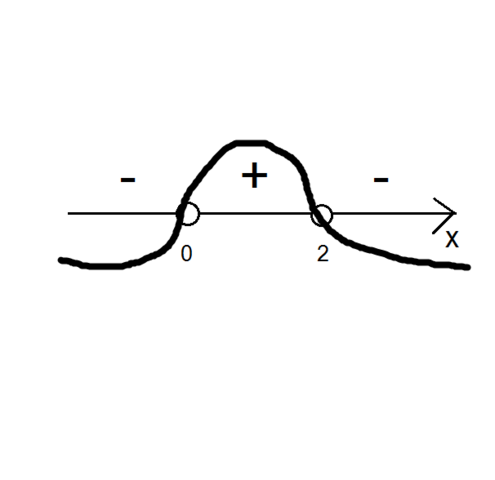
3)Методом интервалов решим неравенства(рисунок во вложении): $I :\frac{x^4+7x^2+12}{2x-x^2} \ \textgreater \ 0 \\ II:\frac{x^4+7x^2+12}{2x-x^2} \ \textless \ 0$

Дробь имеет положительные значения при x∈(0;2).
Дробь имеет отрицательные значения при x∈(-∞;0)v(2;+∞).