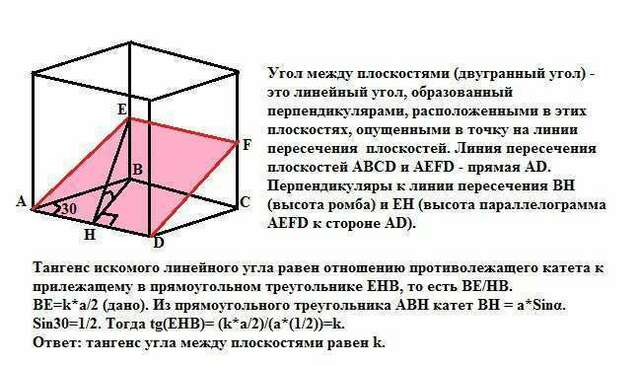
Угол между плоскостями (двугранный угол) - это линейный угол, образованный перпендикулярами, расположенными в этих плоскостях, опущенными в точку на линии пересечения плоскостей. Линия пересечения плоскостей АВСD и AEFD - прямая AD. Перпендикуляры к линии пересечения BН (высота ромба) и ЕН (высота параллелограмма АЕFD к стороне АD).
Тангенс искомого линейного угла равен отношению противолежащего катета к прилежащему в прямоугольном треугольнике ЕНВ, то есть ВЕ/НВ.
ВЕ=k*a/2 (дано). Из прямоугольного треугольника АВН катет ВН = а*Sinα.
Sin30=1/2. Тогда tg(ЕНВ)= (k*a/2)/(а*(1/2))=k.
Ответ: тангенс угла между плоскостями равен k.