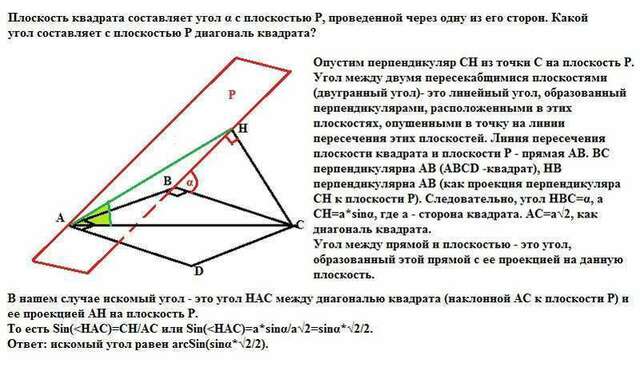
Опустим перпендикуляр СН из точки С на плоскость Р.
Угол между двумя пересекабщимися плоскостями (двугранный угол)- это линейный угол, образованный перпендикулярами, расположенными в этих плоскостях, опушенными в точку на линии пересечения этих плоскостей.
Линия пересечения плоскости квадрата и плоскости Р - прямая АВ.
ВС перпендикулярна АВ (АВСD -квадрат), НВ перпендикулярна АВ (как проекция перпендикуляра СН к плоскости Р).
Следовательно, угол НВС=α, а СН=а*sinα, где а - сторона квадрата. АС=а√2, как диагональ квадрата.
Угол между прямой и плоскостью - это угол, образованный этой прямой с ее проекцией на данную плоскость.
В нашем случае искомый угол - это угол НАС между диагональю квадрата (наклонной АС к плоскости Р) и ее проекцией АН на плоскость Р.
То есть Sin(Ответ: искомый угол равен arcSin(sinα*√2/2).