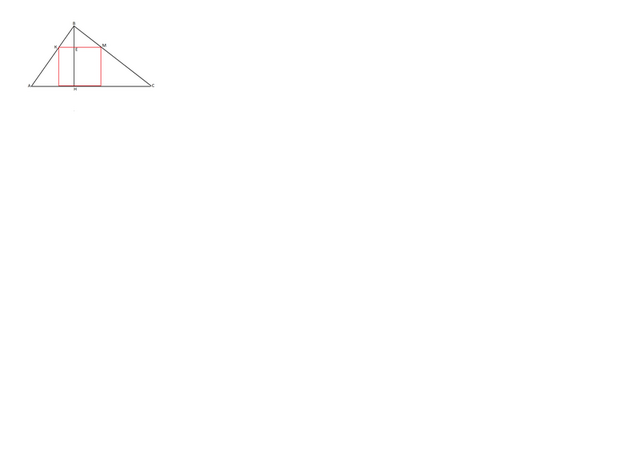
Сделаем рисунок.
Обозначим основание высоты треугольника буквой Н, верхнюю сторону вписанного квадрата КМ, пересечение высоты ВН треугольника со стороной КМ квадрата буквой Е
Стороны квадрата параллельны.
Рассмотрим треугольники АВС и КВМ
Они подобны по равным углам: один общий, другие при параллельных основаниях.
Пусть сторона квадрата КМ=а.
Тогда ВЕ=24-а
Из подобия треугольников справедливо отношение
АВ:КМ=ВН:ВЕ
40:а=24:(24-а)
40*(24-а)=24а
960-40а=24а
960=64а
а= 15 см
Площадь квадрата
S=а²=15²=225 см²