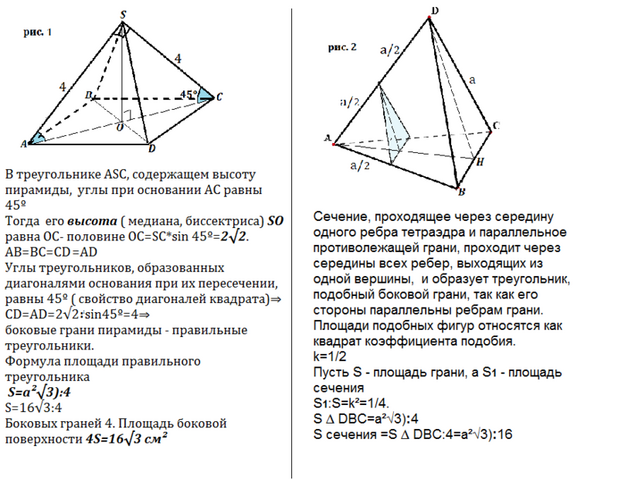
1.Боковое ребро правильной четырёхугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды 45°.
Найти:
а) высоту пирамиды;
б) площадь боковой поверхности пирамиды
-------
Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.
В треугольнике АSС, содержащем высоту пирамиды, углы при основании АС равны 45º
Тогда его медиана ( высота, биссектриса) SO равна ОС- половине ОС=SC:sin 45º=2√2.
Высота пирамиды равна 2√2 см.
AB=BC=CD
Углы треугольников. образованных диагоналями при их пересечении, равны 45º ( свойство диагоналей квадрата)⇒
СD=AD=2√2*sin45º=4⇒
боковые грани пирамиды - правильные треугольники.
Формула площади правильного треугольника
S=a²√3):4
S=16√3:4
Боковых граней 4. Площадь боковой поверхности 4S=16√3 см²
-----------
2. Ребро правильного тетраэдра DABC = а. Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC, и найдите площадь этого сечения.
--
Сечение, проходящее через середину одного ребра тетраэдра и параллельное противолежащей грани, проходит через середины всех ребер, выходящих из одной вершины, и образует треугольник, подобный боковой грани.
Площади подобных фигур относятся как квадрат коэффициента подобия.
k=1/2
Пусть S - площадь грани, а S₁ - площадь сечения
S₁:S=k²=1/4.
S ∆ DBC=a²√3):4
S сечения =S ∆ DBC:4=
a²√3):16