В правильной шестиугольной призме АВСDEFA1B1C1D1E1F1 все ребра равны корень из 2 .Найдите...

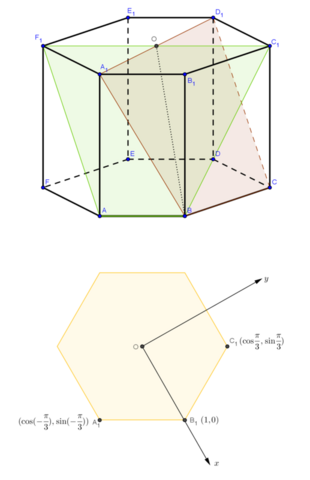
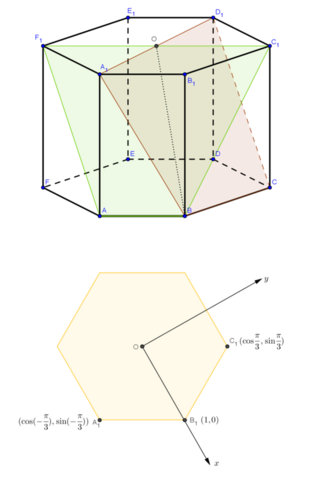
Для упрощения записей буду читать, что все ребра равны единице - все равно углы останутся прежними.

Введем ПСК с началом координат в центре нижнего основания (см. рисунок). Будем искать уравнения плоскостей. Уравнения имеют вид Xx+Yy+Zz=D.

Координаты точек:

$A(-\frac12,\frac{\sqrt3}2,0);\;C(\frac12,\frac{\sqrt3}2,0); \;B(1,0,0);\;O(0,0,1)$

Плоскости a1 принадлежат точки B, C, O; поэтому ее уравнение находится из системы

$\begin{cases} X=D\\ \frac12X+\frac{\sqrt3}2Y=D\\ Z=D \end{cases}$

Решив систему, получаем уравнение плоскости

$\sqrt3x+y+\sqrt3z=\sqrt3$

Аналогично, для второй плоскости

$x+\sqrt3y+z=1$

Отсюда получаем вектора нормалей для плоскостей:

$\vec{n}_1=(\sqrt3,1,\sqrt3)$

$\vec{n}_2=(1,\sqrt3,1)$

По формуле, можно найти косинус угла между плоскостями:

$\cos(\alpha_1,\alpha_2)=\dfrac{|\vec n_1\cdot\vec n_2|}{|\vec n_1||\vec n_2|}=\dfrac{3\sqrt3}{7\cdot5}=\dfrac{3\sqrt3}{35}$

Искомый угол - арккосинус.