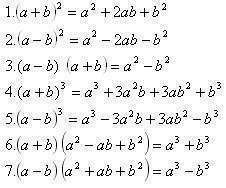Способ 1. Вынесение общего множителя за скобку.
ac + bc = c(a + b).
Способ 2. Использование формул сокращенного умножения.
Смотри во вложении.
Способ 3. Группировка.
Способ группировки заключается в объединение компонентов многочлена таким образом, чтобы над ними было легко совершать действия (сложение, вычитание, вынесение общего множителя).
Пример.
Разложим на множители многочлен х3 – 3х2 + 5х – 15.
Решение.
1. Сгруппируем компоненты таким образом: 1-ый со 2-ым, а 3-ий с 4-ым
(х3 – 3х2) + (5х – 15).
2. В получившемся выражении вынесем общие множители за скобки: х2 в первом случае и 5 – во втором.
(х3 – 3х2) + (5х – 15) = х2(х – 3) + 5(х – 3).
3. Выносим за скобки общий множитель х – 3 и получаем:
х2(х – 3) + 5(х – 3) = (х – 3)( х2 + 5).
Итак,
х3 – 3х2 + 5х – 15 = (х3 – 3х2) + (5х – 15) = х2(х – 3) + 5(х – 3) = (х – 3) ∙ ( х2 + 5).