Катеты прямоугольного треугольника ABC имеют длину 60 см и 80 см. Из вершины C прямого...

Question

Катеты прямоугольного треугольника ABC имеют длину 60 см и 80 см. Из вершины C прямого угла к плоскости треугольника восстановлен перпендикуляр CD = 36 см. Найдите угол наклона DF к плоскости треугольника, где DF - перпендикуляр, опущенный из точки D на прямую AB.

Answer 1

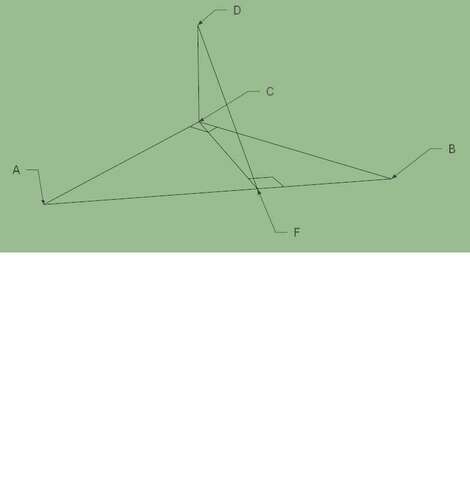
Рассмотрим ΔAFC и ΔACB оба прямоугольные (∠F=∠C), так же в них общий угол А, значит треугольники подобны (по трем углам). Составим соотношение сторон: AF/AC=CA/AB. АВ найдем по т. Пифагора АВ²=60²+80², АВ=100. Теперь подставим все в соотношение:
AF/60=60/100, AF=36. Теперь рассмотрим ΔAFC он прямоугольный, тогда АС²=CF²+AF², 60²=CF²+36², отсюда CF=48. 
Теперь осталось рассмотреть ΔFCD он тоже прямоугольный значит DF²=DC²+CF², DF²=36²+48², DF=60.

---