Формула объёма конуса
V=S*h/3
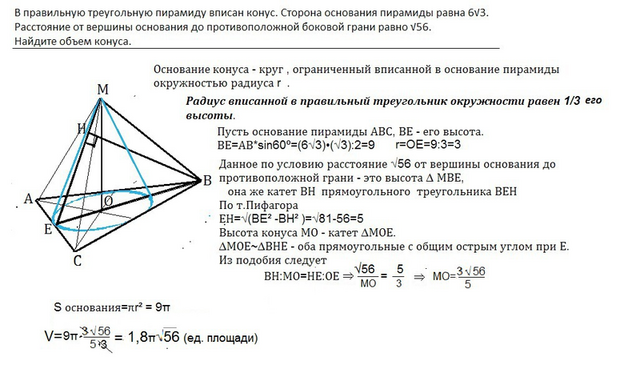
Его основание - круг , ограниченный вписанной в основание пирамиды окружностью радиуса r .
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты.
Пусть основание пирамиды АВС, ВЕ - его высота.
ВЕ=АВ*sin 60º=(6√3)•(√3):2=9⇒
r=OE=9:3=3
Данное по условию расстояние √56 от вершины основания до противоположной грани - это высота ∆ МВЕ, она же катет ВН прямоугольного треугольника ВЕН
По т.Пифагора
ЕН=√(BE² -BH² )=√81-56=5
Высота конуса МО - катет ∆МОЕ.
∆МОЕ~∆ВНЕ - оба прямоугольные с общим острым углом при Е.
Из подобия следует отношение:
ВН:МО=НЕ:ОЕ
√56:МО=5:3
5МО=3√56
МО=(3√56):5
S основания=πr² = 9π
V=[(9π•3√56):5]:3=1,8π√56 (ед. площади)